My Test Tube Filled with DNA is Better than Your Mesos Cluster
We’ve seen computation using slime mold, soap film, water droplets, there’s even a 10,000 Domino Computer. Now DNA can do math In a test tube. Using addition, subtraction, multiplication, and division.
It’s not fast. Calculations can take hours. The upside: they are tiny and can work in wet environments. Think of running calculations in your bloodstream or in cells, like a programmable firewall, to monitor and alert on targeted health metrics and then trigger a localized response. Or if you are writing science fiction perhaps the ocean could become one giant computer?
The applications already sound like science fiction:
Prior devices for control of chemical reaction networks and DNA doctor applications have been limited to finite-state control, and analog DNA circuits will allow much more sophisticated analog signal processing and control. DNA robotics have allowed devices to operate autonomously (e.g., to walk on a nanostructure) but also have been limited to finite-state control.
Analog DNA circuits can allow molecular robots to include real-time analog control circuits to provide much more sophisticated control than offered by purely digital control. Many artificial intelligence systems (e.g., neural networks and probabilistic inference) that dynamically learn from environments require analog computation, and analog DNA circuits can be used for back-propagation computation of neural networks and Bayesian probabilistic inference systems.
How does it work?
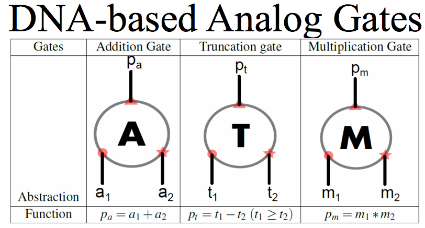
Strands of synthetic DNA that, when mixed together in a test tube in the right concentrations, form an analog circuit that can add, subtract and multiply as they form and break bonds. Rather than voltage, DNA circuits use the concentrations of specific DNA strands as signals. Researchers solve math problems by measuring the concentrations of specific outgoing strands as the reaction reaches equilibrium.
It took a little digging, but I found a non-paywall version of the source paper: Analog Computation by DNA Strand Displacement Circuits. It's a well written paper, but it's way above my pay grade technically. If you want an overview of the entire space then here’s a really great presentation: DNA Circuits for Analog Computing.
Some extracts:
What is DNA computing?
DNA computing is using DNA as hardware to perform computing [1]. The computing is usually based on DNA hybridization and DNA strand displacement.
Why are we interested in DNA computing?
DNA is a highly programmable biological material based on Watson-Crick base pairs (A-T, G-C). We can control the reaction pathway and kinetics of DNAbased system by programming the sequences. Large scale DNA-based digital circuits have been demonstrated [1].
Potential Applications of DNA Circuits for Analog Computing
Analog circuits need less gates to perform arithmetic operation. For example, we only need one gate for each arithmetic operation (addition, subtraction and multiplication) in analog system. In digital system, we need several gates. This property makes analog DNA circuits be useful in resource-limited environment e.g. in living cells
Nature operates in a hybrid of analog and digital fashion [2]. Analog DNA circuits can serve as interface to natural analog systems.
Why Analog?
Analog circuits have their advantages over digital circuits. For example, analog circuits require much fewer gates to conduct numerical computation up to a given accuracy compared to their digital counterparts. Elementary arithmetic operations such as addition, subtraction, and multiplication are computed by single gates in analog circuits, whereas digital circuits require multiple gates for each elementary arithmetic operation. It means that analog circuits consume less resources than corresponding digital circuits and this property makes analog circuits useful in resource limited environments (e.g., in living cells). Furthermore, for some applications, analog circuits can be more robust than digital circuits.
You can Build Circuits
Circuits to Compute Polynomial Functions:
- Strategy: connect gates together by simply programming the sequence of output strand of a gate.
- Potential Problem: static input vs. dynamic input
- Tricks: use static input for Im2 input of all multiplication gates to set up the concentration ratio between G’m3 and Gm4 as soon.
Beyond Polynomial Functions: Taylor Series and Newton Iteration
- The formula assigned to each wire describes the signal that goes through it. Each gate is assigned a number for the convenience to describe the circuit design. The input range of gate-2, gate-4, gate-5, gate-6, gate-7 and gate-8 is 1. The input range of gate-1 is 4. The input range of gate-3 is 2. The input ranges are determined by the upper bound of input signals of a gate and we use the gates with the input ranges that we tested by simulation